Quantum-Hybrid Stereo Matching With Nonlinear Regularization and Spatial Pyramids

Quantum visual computing is advancing rapidly. This paper presents a new formulation for stereo matching with nonlinear regularizers and spatial pyramids on quantum annealers as a maximum a posteriori inference problem that minimizes the energy of a Markov Random Field. Our approach is hybrid (i.e., quantum-classical) and is compatible with modern D-Wave quantum annealers, i.e., it includes a quadratic unconstrained binary optimization (QUBO) objective. Previous quantum annealing techniques for stereo matching are limited to using linear regularizers, and thus, they do not exploit the fundamental advantages of the quantum computing paradigm in solving combinatorial optimization problems. In contrast, our method utilizes the full potential of quantum annealing for stereo matching, as nonlinear regularizers create optimization problems which are NP-hard. On the Middlebury benchmark, we achieve an improved root mean squared accuracy over the previous state of the art in quantum stereo matching of 2% and 22.5% when using different solvers.

Stereo estimates on the Middlebury Venus stereo image pair. From left to right: Heidari et al.’s approach, our approach and ground truth. In this example, we achieve a 46% decrease in root mean squared error (RMSE) from Heidari et al. and a 10% decrease in bad pixel percentage (BPP). We avoid many of the streaking artifacts present in the result of the prior approach.

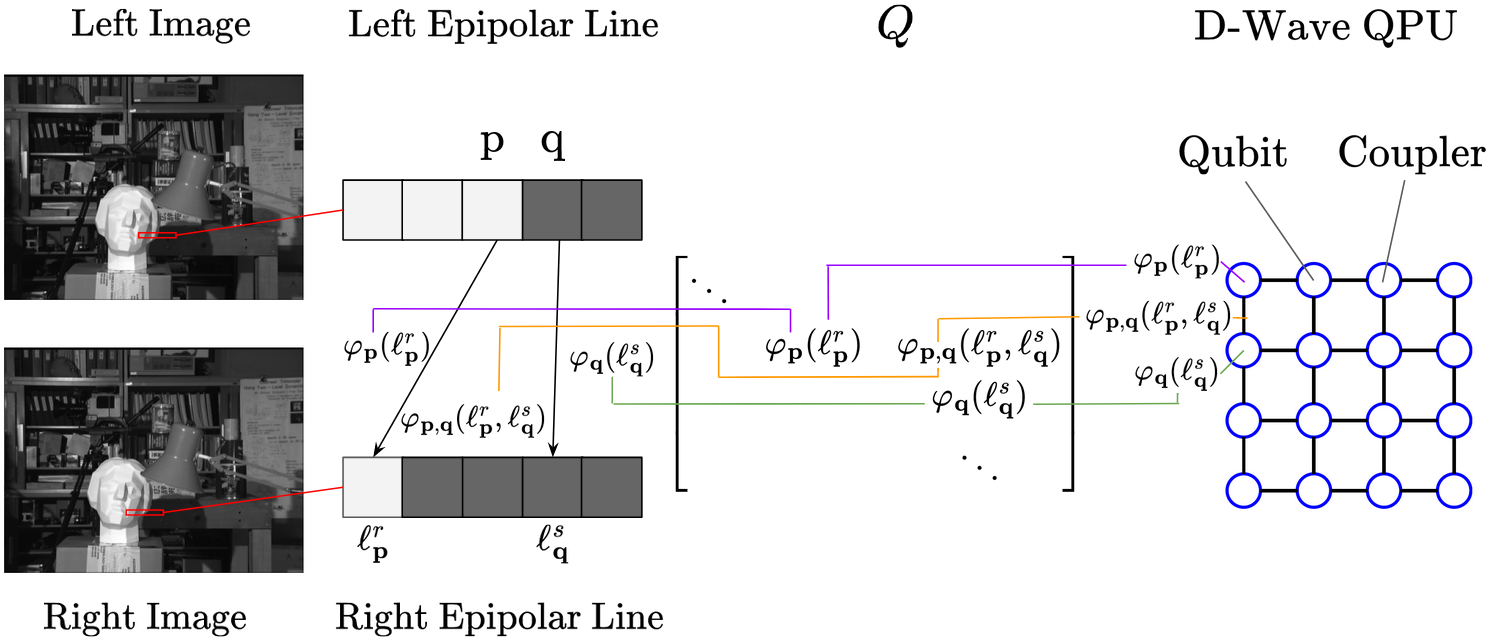
We zoom in on the corresponding epipolar lines for the Tsukuba image pair. For pixels with Markov variables p and q, we consider their respective displacement labels ℓ ^r _p and ℓ ^s _q. We classically calculate the data costs φ _p (ℓ ^r _p ) and φ _q (ℓ ^s _q ), and the regularization cost φ _p,q (ℓ ^r _p , ℓ ^s _q ) . These values are then processed into the QUBO matrix Q, which is then used to set the qubit and coupler energies on the D-Wave QPU. The diagram only sketches how these cost values calculated from the image pair are programmed into the QPU. Numerical details of the QUBO encoding scheme in Q and minor embedding in the D-Wave QPU have been omitted for the sake of simplicity. Please refer to our full paper for more details.