Q-Match: Iterative Shape Matching via Quantum Annealing

Abstract

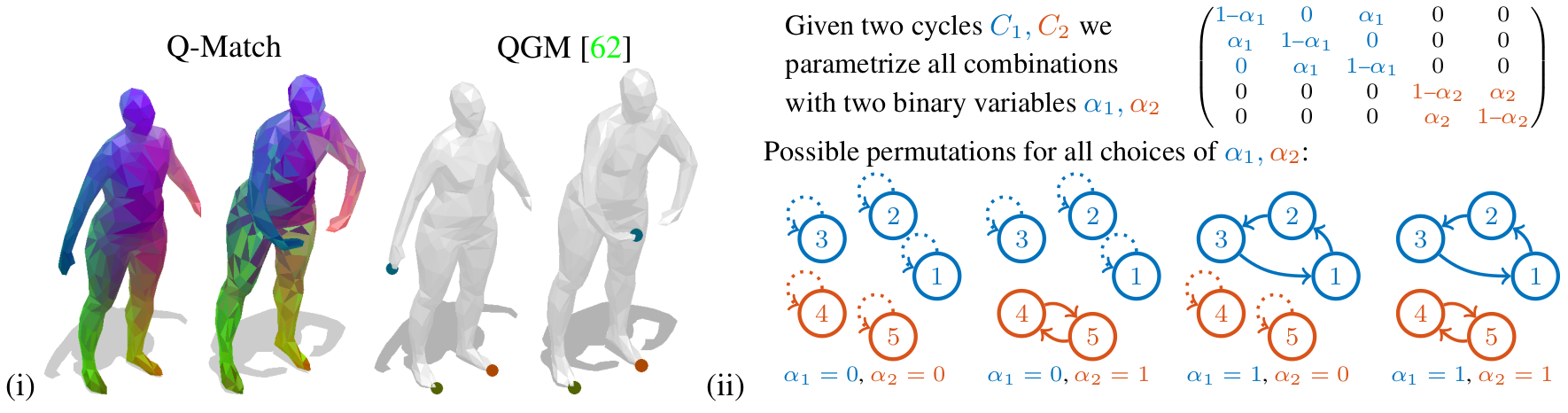
Finding shape correspondences can be formulated as an NP-hard quadratic assignment problem (QAP) that becomes infeasible for shapes with high sampling density. A promising research direction is to tackle such quadratic optimization problems over binary variables with quantum annealing, which, in theory, allows to find globally optimal solutions relying on a new computational paradigm. Unfortunately, enforcing the linear equality constraints in QAPs via a penalty significantly limits the success probability of such methods on currently available quantum hardware. To address this limitation, this paper proposes Q-Match, i.e., a new iterative quantum method for QAPs inspired by the α-expansion algorithm, which allows solving problems of an order of magnitude larger than current quantum methods. It works by implicitly enforcing the QAP constraints by updating the current estimates in a cyclic fashion. Further, Q-Match can be applied for shape matching problems iteratively, on a subset of well-chosen correspondences, allowing us to scale to real-world problems. Using the latest quantum annealer, the D-Wave Advantage, we evaluate the proposed method on a subset of QAPLIB as well as on isometric shape matching problems from the FAUST dataset.