Unbiased 4D: Monocular 4D Reconstruction with a Neural Deformation Model

Abstract

Capturing general deforming scenes is crucial for many applications in computer graphics and vision, and it is especially challenging when only a monocular RGB video of the scene is available. Competing methods assume dense point tracks over the input views, 3D templates, large-scale training datasets, or only capture small-scale deformations. In stark contrast to those, our method makes none of these assumptions while significantly outperforming the previous state of the art in challenging scenarios. Moreover, our technique includes two new—in the context of non-rigid 3D reconstruction—components, i.e., 1) A coordinate-based and implicit neural representation for non-rigid scenes, which enables an unbiased reconstruction of dynamic scenes, and 2) A novel dynamic scene flow loss, which enables the reconstruction of larger deformations. Results on our new dataset, which will be made publicly available, demonstrate the clear improvement over the state of the art in terms of surface reconstruction accuracy and robustness to large deformations.

Video

Method

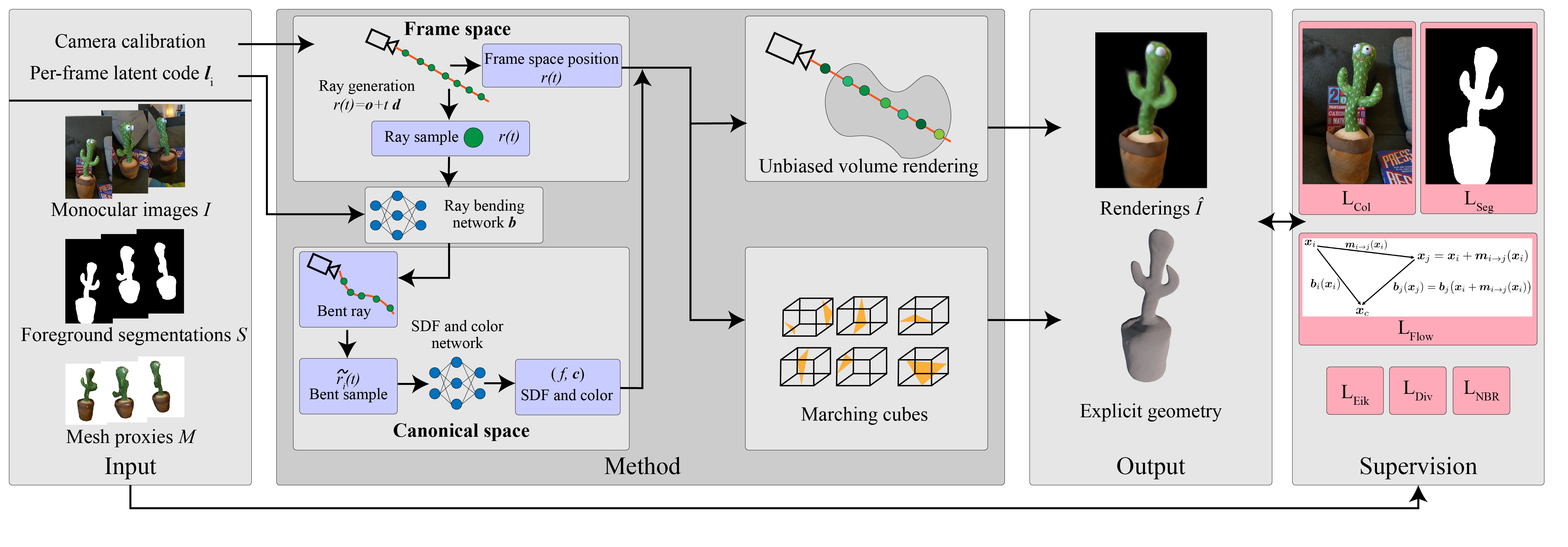
Given calibrated monocular RGB images and segmentations, along with an optional mesh geometric proxy, Ub4D jointly learns a canonical scene representation and a per-frame deformation into that canonical space. We propose a rendering method that is provably unbiased for bent rays in canonical space and uses an SDF to avoid the surface ambiguity present in density formulations. Additionally, for challenging scenes, we propose a novel scene flow loss that supervises the per-frame deformation field through the use of a coarse geometric proxy. This scene flow loss allows Ub4D to resolve multiple canonical copies of object geometry that require additional object or scene priors (see example below).

Above: Column 1 shows the input image for our Humanoid dataset, column 2 shows the results without our scene flow loss (note the duplicated arms), column 3 shows the SMPL proxy, and column 4 shows the result using our scene flow loss. Note that actually only a sparse set of points are necessary as we show in supplementary material and on this page below.

Datasets

We introduce five new datasets demonstrating non-rigidly deforming objects with large camera baseline motion: Cactus, RootTrans, Lego, Humanoid, and RealCactus. Three are synthetic with ground truth camera parameters, while two are real-world captures with camera parameters estimated using COLMAP. Two of the synthetic datasets and one of the real-world captures include geometric proxies. Note that the two scenes not requiring geometric proxies include an initially rigid portion.

Cactus

RootTrans

Lego

Humanoid

RealCactus

Results

We show video results demonstrating the reconstruction results of Ub4D for each dataset. The colored reconstructions are generated by querying the rendering network using the normal vector as the viewing direction and are only for visualization purposes.

Above: Column 1 shows the input images, column 2 shows the input proxies, column 3 overlays the output on the input images, column 4 overlays the error maps on the input images (dark blue is zero error, red is high error), and column 5 shows the colored reconstruction result.

Above: Column 1 shows the input images, column 2 gives the reconstruction result, column 3 shows a colored reconstruction, and column 4 presents the colored reconstruction from a fixed camera view.

Above: Column 1 shows the input images, column 2 shows the input proxies, column 3 gives the reconstruction result, column 4 presents the colored reconstruction, and column 5 gives the colored reconstruction from a fixed camera view.

Above: Column 1 shows the input images, column 2 gives the reconstruction result, and columns 3 and 4 show the color reconstruction from two fixed camera views.

Geometric Proxy Resolution Ablation

We have identified that the geometric proxy does not need to have a very high resolution and show examples in our supplementary material. We demonstrate this by using a proxy with just 7 vertices selected from the SMPL proxies: one on each extremity, two on the body, and one on the head. This sufficiently summarizes the motion of the human character scenes in order to eliminate duplication (both of the character and of the arms) in the canonical space. This suggests the use of a 3D skeleton proxy rather than a complete mesh proxy.

Above: Column 1 shows the input image for our RootTrans dataset, column 2 shows the output using the full SMPL proxy, column 3 shows the output using only 7 vertices of the SMPL proxy, and column 4 shows the output without using the scene flow loss. The second row shows the same, but from a novel view and with frustum culling disabled. Note the multiple object copies in column 4 are rotated in and out of the camera frustum, whereas the torso tower in columns 2 and 3 is never placed in the camera frustum.

Latent Code Analysis and Novel Geometry Synthesis

We show an analysis of the learned latent codes in our supplementary material. Note that the latent code can be seen as a factorization of all time-dependent geometry changes in the scene given that it is the only element of our method that varies with the frames of the input.

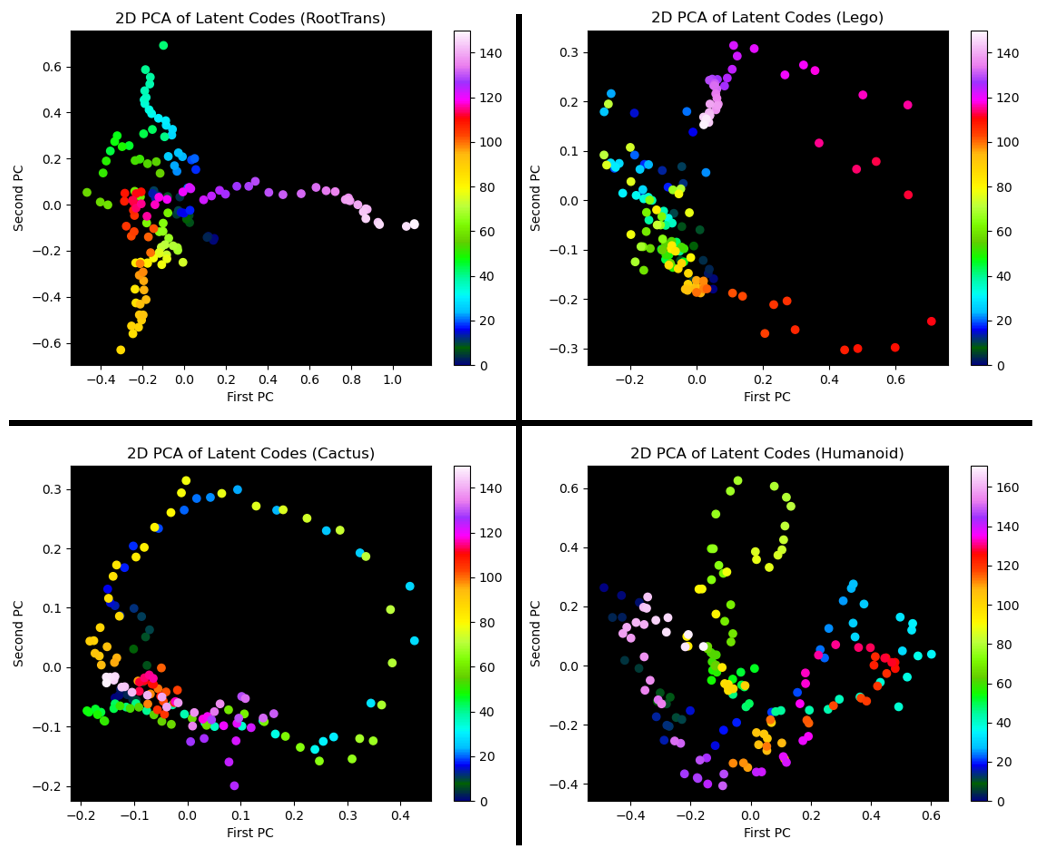
Above: Result of performing PCA on the learned latent codes for four of our datasets. Colors represent frame indices. Note that nearby frames (similar colors) are nearby in the projection validating semantic meaning of the latent codes. Further examining the latent projection along with the input images shows that similar geometrical states are nearby.

We also validate the decision to initialize the latent codes with zero (as suggested by NR-NeRF) and show that this along creates semantically meaningful latent codes. We cannot do this analysis with a projection so we use 2D latent codes.

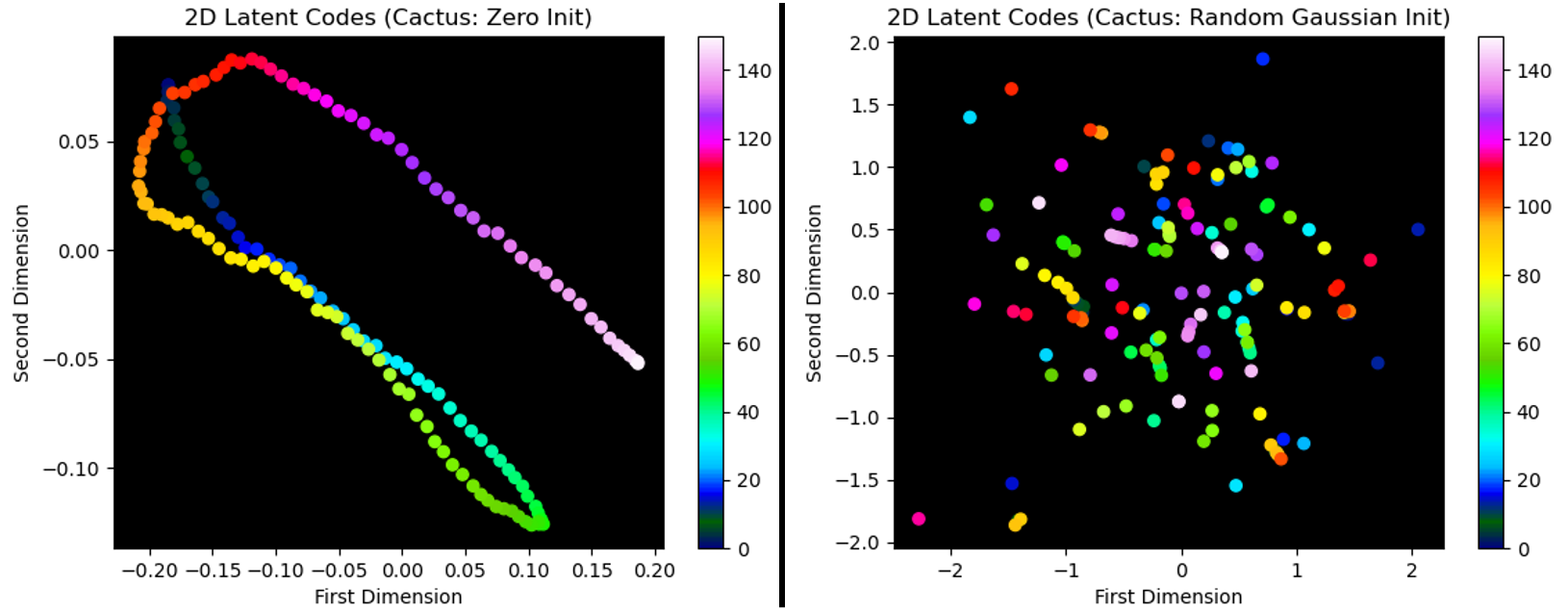
Above: Comparison of zero and random Gaussian latent code initialization using 2D latent codes. Colors represent frame indices. Note the structuring of the zero-initialized latent codes, particularly in light of its relation to the true geometric scene state. This validates the use of latent codes for scene understanding (identifying similar non-rigid object states viewed from different camera positions), as well as for novel geometry synthesis which we show below. Lower dimensional latent codes do not decrease the quantitative error of the reconstruction.

Above: Example of generating novel geometry by providing a new latent code (red dot). The grey dots show the observed Note how the smoothness of the latent space extends outside even the convex hull of the observed states.

Novel View Synthesis

While Ub4D does not target the application of novel view synthesis, we shows results here to highlight some shortcomings when our method is used for this application.

Above: Column 1 shows the input image, column 2 shows the render from the camera view, and column 3 gives the render from a fixed view.

Above: Note the noise around the edges of the object. This may be due to having no direct spatial gradient regularization on the bending network or sampling issues due to narrowing surface width (value of s) over training.

Citation

@inproceedings{johnson2023ub4d,
	title={Unbiased 4D: Monocular 4D Reconstruction with a Neural Deformation Model}, 
	author={Erik C.M. Johnson and Marc Habermann and Soshi Shimada and Vladislav Golyanik and Christian Theobalt},
	year={2023},
	booktitle = {Computer Vision and Pattern Recognition Workshops (CVPRW)}, 
}