CCuantuMM: Cycle-Consistent Quantum-Hybrid Matching of Multiple Shapes
Abstract
Jointly matching multiple, non-rigidly deformed 3D shapes is a challenging, NP-hard problem. A perfect matching is necessarily cycle-consistent: Following the pairwise point correspondences along several shapes must end up at the starting vertex of the original shape. Unfortunately, existing quantum shape-matching methods do not support multiple shapes and even less cycle consistency. This paper addresses the open challenges and introduces the first quantum-hybrid approach for 3D shape multi-matching; in addition, it is also cycle-consistent. Its iterative formulation is admissible to modern adiabatic quantum hardware and scales linearly with the total number of input shapes. Both these characteristics are achieved by reducing the N-shape case to a sequence of three-shape matchings, the derivation of which is our main technical contribution. Thanks to quantum annealing, high-quality solutions with low energy are retrieved for the intermediate NP-hard objectives. On benchmark datasets, the proposed approach significantly outperforms extensions to multi-shape matching of a previous quantum-hybrid two-shape matching method and is on-par with classical multi-matching methods.
Quantum Annealing
The proposed approach in this paper introduces a novel iterative algorithm that employs a quantum annealer from D-Wave in each step to address the challenges of multi-matching non-rigidly deformed 3D shapes. The algorithm uses a metaheuristic method, quantum annealing, to efficiently search the energy landscape of the cost function. Current generation quantum annealer possess the ability to solve only quadratic unconstrained binary optimization (QUBO) problems. The proposed algorithm converts the Quadratic Assignment Problem with permutation constraints to a QUBO. This method offers a significant improvement over previous quantum-hybrid two-shape matching methods extended to multi-shape matching and is on par with classical multi-matching methods, making it a promising solution for the challenging task of matching multiple non-rigidly deformed 3D shapes.
Talk
Evolution
Figure 2: This demonstrates the progression of point-wise correspondences using our approach.
Specifically, we present the outcomes obtained from running the method on a 10 shape FAUST instance for a total of 198 iterations.
Please note that the video may only be supported in chrome.
Results
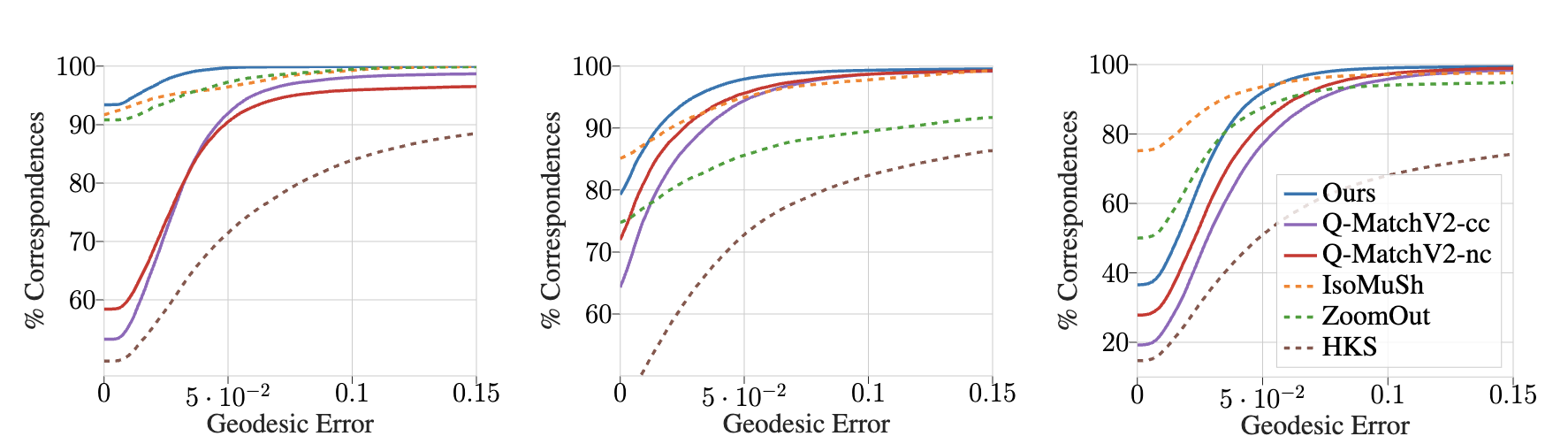
Figure 3: Quantitative results on all three datasets (left) FAUST, (middle) TOSCA, and (right) SMAL. For each dataset, we match all shapes within a class and then plot the average PCK curve across classes. We plot classical methods with dashed lines as they are only for reference. HKS is our initialisation.
| Ours | Q-MatchV2-cc | Q-MatchV2-nc | IsoMuSH | ZoomOut | HKS | |
|---|---|---|---|---|---|---|
| FAUST | 0.989 | 0.886 | 0.879 | 0.974 | 0.886 | 0.746 |
| TOSCA | 0.967 | 0.932 | 0.940 | 0.952 | 0.864 | 0.742 |
| SMAL | 0.866 | 0.771 | 0.813 | 0.926 | 0.851 | 0.544 |
Table 1: AUC averaged over all classes of each dataset. For reference, we also include classical methods on the right.
Downloads
Citation
@inproceedings{bhatia2023CCuantuMM,
title = {CCuantuMM: Cycle-Consistent Quantum-Hybrid Matching of Multiple Shapes},
author = {Bhatia, Harshil and Tretschk, Edith and Lähner, Zorah and Seelbach Benkner,
Marcel and Möller, Michael and Theobalt, Christian and Golyanik, Vladislav },
year = {2023},
booktitle = {{IEEE Conference on Computer Vision and Pattern Recognition (CVPR)}},
keywords = {Shape Analysis, Geometry Processing, Shape Correspondence,
Multi Shape Matching},
}
Contact
For questions, clarifications, please get in touch with:Harshil Bhatia bhatia.2@iitj.ac.in, hbhatia@mpi-inf.mpg.de
Vladislav Golyanik golyanik@mpi-inf.mpg.de



